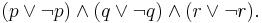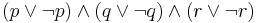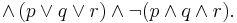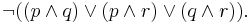Answer set programming

Agent-oriented
Automata-based
Component-based
- Flow-based
- Pipelined
Concatenative
Concurrent computing
- Relativistic programming
Data-driven
Declarative (contrast: Imperative)
- Constraint
- Dataflow
  - Cell-oriented (spreadsheets)
  - Reactive
- Logic
  - Abductive logic
  - Answer set
  - Constraint logic
  - Functional logic
  - Inductive logic
Event-driven
- Service-oriented
- Time-driven
Expression-oriented
Feature-oriented
Function-level (contrast: Value-level)
Functional
Generic
Imperative (contrast: Declarative)
- Procedural
Language-oriented
- Discipline-specific
- Domain-specific
- Grammar-oriented
  - Dialecting
- Intentional
Metaprogramming
- Automatic
- Reflective
  - Attribute-oriented
- Template
  - Policy-based
Non-structured (contrast: Structured)
- Array
Nondeterministic
Parallel computing
- Process-oriented
Programming in the large / small
Semantic
Structured (contrast: Non-structured)
- Modular (contrast: Monolithic)
- Object-oriented
- Recursive
Value-level (contrast: Function-level)

Answer set programming (ASP) is a form of declarative programming oriented towards difficult (primarily NP-hard) search problems. It is based on the stable model (answer set) semantics of logic programming. In ASP, search problems are reduced to computing stable models, and answer set solvers -- programs for generating stable models—are used to perform search. The computational process employed in the design of many answer set solvers is an enhancement of the DPLL algorithm and, in principle, it always terminates (unlike Prolog query evaluation, which may lead to an infinite loop).

In a more general sense, ASP includes all applications of answer sets to knowledge representation^[1]^[2] and the use of Prolog-style query evaluation for solving problems arising in these applications.

1 History
2 Answer set programming language AnsProlog
3 Generating stable models
4 Examples of ASP programs
5 Comparison of implementations
6 See also
7 References
8 External links

History

The planning method proposed by Dimopoulos, Nebel and Köhler^[3] is an early example of answer set programming. Their approach is based on the relationship between plans and stable models.^[4] Soininen and Niemelä^[5] applied what is now known as answer set programming to the problem of product configuration. The use of answer set solvers for search was identified as a new programming paradigm in Marek and Truszczyński^[6] (the term "answer set programming" was used for the first time as the title of a part of the collection where that paper appeared) and in [Niemelä 1999].^[7]

Answer set programming language AnsProlog

Lparse is the name of the program that was originally created as grounding tool (front-end) for the answer set solver smodels. The language that Lparse accepts is now commonly called AnsProlog*^[8], short for Answer Set Programming in Logic^[9]. It is now used in the same way in many other answer set solvers, including assat, clasp, cmodels, gNt, nomore++ and pbmodels. (dlv is an exception; the syntax of ASP programs written for dlv is somewhat different.)

An AnsProlog program consists of rules of the form

<head> :- <body> .

The symbol :- ("if") is dropped if <body> is empty; such rules are called facts. The simplest kind of Lparse rules are rules with constraints.

One other useful construct included in this language is choice. For instance, the choice rule

{p,q,r}.

says: choose arbitrarily which of the atoms 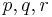$p,q,r$ to include in the stable model. The lparse program that contains this choice rule and no other rules has 8 stable models—arbitrary subsets of 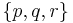$\{p,q,r\}$ . The definition of a stable model was generalized to programs with choice rules.^[10] Choice rules can be treated also as abbreviations for propositional formulas under the stable model semantics.^[11] For instance, the choice rule above can be viewed as shorthand for the conjunction of three "excluded middle" formulas:

$(p\lor\neg p)\land(q\lor\neg q)\land(r\lor\neg r).$

The language of lparse allows us also to write "constrained" choice rules, such as

1{p,q,r}2.

This rule says: choose at least 1 of the atoms 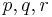$p,q,r$ , but not more than 2. The meaning of this rule under the stable model semantics is represented by the propositional formula

$(p\lor\neg p)\land(q\lor\neg q)\land(r\lor\neg r)$

$\land\,(p\lor q\lor r)\land\neg(p\land q\land r).$

Cardinality bounds can be used in the body of a rule as well, for instance:

:- 2{p,q,r}.

Adding this constraint to an Lparse program eliminates the stable models that contain at least 2 of the atoms 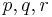$p,q,r$ . The meaning of this rule can be represented by the propositional formula

$\neg((p\land q)\lor(p\land r)\lor(q\land r)).$

Variables (capitalized, as in Prolog) are used in Lparse to abbreviate collections of rules that follow the same pattern, and also to abbreviate collections of atoms within the same rule. For instance, the Lparse program

p(a). p(b). p(c).
q(X) :- p(X), X!=a.

has the same meaning as

p(a). p(b). p(c).
q(b). q(c).

The program

p(a). p(b). p(c).
{q(X):p(X)}2.

is shorthand for

p(a). p(b). p(c).
{q(a),q(b),q(c)}2.

Generating stable models

To find a stable model of the Lparse program stored in file <filename> we use the command

% lparse <filename> | smodels

Option 0 instructs smodels to find all stable models of the program. For instance, if file test contains the rules

1{p,q,r}2.
s :- not p.

then the command

% lparse test | smodels 0

produces the output

Answer: 1
Stable Model: q p 
Answer: 2
Stable Model: p 
Answer: 3
Stable Model: r p 
Answer: 4
Stable Model: q s 
Answer: 5
Stable Model: r s 
Answer: 6
Stable Model: r q s

Examples of ASP programs

Graph coloring

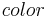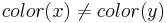An $n$ -coloring of a graph $G$ is a function $color\$ from its set of vertices to $\{1,\dots,n\}$ such that $color(x)\neq color(y)$ for every pair of adjacent vertices 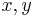$x,y$ . We would like to use ASP to find an $n$ -coloring of a given graph (or determine that it does not exist).

This can be accomplished using the following Lparse program:

c(1..n).                                           
1 {color(X,I) : c(I)} 1 :- v(X).             
:- color(X,I), color(Y,I), e(X,Y), c(I).

Line 1 defines the numbers $1,\dots,n$ to be colors. According to the choice rule in Line 2, a unique color $i$ should be assigned to each vertex $x$ . The constraint in Line 3 prohibits assigning the same color to vertices $x$ and $y$ if there is an edge connecting them.

If we combine this file with a definition of $G$ , such as

v(1..100). % 1,...,100 are vertices
e(1,55). % there is an edge from 1 to 55
. . .

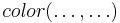and run smodels on it, with the numeric value of $n$ specified on the command line, then the atoms of the form $color(\dots,\dots)$ in the output of smodels will represent an $n$ -coloring of $G$ .

The program in this example illustrates the "generate-and-test" organization that is often found in simple ASP programs. The choice rule describes a set of "potential solutions" -- a simple superset of the set of solutions to the given search problem. It is followed by a constraint, which eliminates all potential solutions that are not acceptable. However, the search process employed by smodels and other answer set solvers is not based on trial and error.

Large clique

A clique in a graph is a set of pairwise adjacent vertices. The following lparse program finds a clique of size 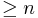$\geq n$ in a given graph, or determines that it does not exist:

n {in(X) : v(X)}.
:- in(X), in(Y), v(X), v(Y), X!=Y, not e(X,Y), not e(Y,X).

This is another example of the generate-and-test organization. The choice rule in Line 1 "generates" all sets consisting of 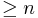$\geq n$ vertices. The constraint in Line 2 "weeds out" the sets that are not cliques.

Hamiltonian cycle

A Hamiltonian cycle in a directed graph is a cycle that passes through each vertex of the graph exactly once. The following Lparse program can be used to find a Hamiltonian cycle in a given directed graph if it exists; we assume that 0 is one of the vertices.

{in(X,Y)} :- e(X,Y).

:- 2 {in(X,Y) : e(X,Y)}, v(X).
:- 2 {in(X,Y) : e(X,Y)}, v(Y).

r(X) :- in(0,X), v(X).
r(Y) :- r(X), in(X,Y), e(X,Y).

:- not r(X), v(X).

The choice rule in Line 1 "generates" all subsets of the set of edges. The three constraints "weed out" the subsets that are not Hamiltonian cycles. The last of them uses the auxiliary predicate 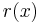$r(x)$ (" $x$ is reachable from 0") to prohibit the vertices that do not satisfy this condition. This predicate is defined recursively in Lines 4 and 5.

This program is an example of the more general "generate, define and test" organization: it includes the definition of an auxiliary predicate that helps us eliminate all "bad" potential solutions.

Comparison of implementations

Early systems, such as Smodels, used backtracking to find solutions. As the theory and practice of Boolean SAT solvers evolved, a number of ASP solvers were built on top of SAT solvers, including ASSAT and Cmodels. These converted ASP formula into SAT propositions, applied the SAT solver, and then converted the solutions back to ASP form. More recent systems, such as Clasp, use a hybrid approach, using conflict-driven algorithms inspired by SAT, without full converting into a boolean-logic form. These approaches allow for significant improvements of performance, often by an order of magnitude, over earlier backtracking algorithms.

The Potassco project acts as an umbrella for many of the systems below, including clasp, grounding systems (gringo), incremental systems (iclingo), constraint solvers (clingcon), action language to ASP compilers (coala), distributed MPI implementations (claspar), and many others.

Most systems support variables, but only indirectly, by forcing grounding, by using a grounding system such as Lparse or gringo as a front end. The need for grounding can cause a combinatorial explosion of clauses; thus, systems that perform on-the-fly grounding might have an advantage.

Platform			Features					Mechanics
Name	OS	Licence	Variables	Function symbols	Explicit sets	Explicit lists	Disjuntive (choice rules) support
ASPeRiX	Linux	GPL	Yes				No	on-the-fly grounding
ASSAT	Solaris	Freeware						SAT-solver based
Clasp Answer Set Solver	Linux, Mac OS, Windows	GPL	yes, in Clingo	Yes	No	No	Yes, in ClaspD	Incremental, SAT-inspired (nogood, conflict-driven)
Cmodels	Linux, Solaris	GPL	Requires grounding				Yes	Incremental, SAT-solver inspired (nogood conflict-driven)
DLV	Linux, Mac OS, Windows^[12]	free for academic and non-commerical educational use, and for non-profit organizations^[12]	Yes	Yes	No	No	Yes	Not Lparse compatible
DLV-Complex	Linux, Mac OS, Windows	Freeware		Yes	Yes	Yes	Yes	Built on top of DLV - Not Lparse compatible
GnT	Linux	GPL	Requires grounding				Yes	built on top of smodels.
nomore++	Linux	GPL						combined literal+rule-based
Platypus	Linux, Solaris, Windows	GPL						Distributed, multi-threaded nomore++, smodels
Pbmodels	Linux	?						Pseudo-boolean solver based
Smodels	Linux, Mac OS, Windows	GPL	Requires grounding	No	No	No	No
Smodels-cc	Linux	?	Requires grounding					SAT-solver based; smodels w/conflict clauses.
Sup	Linux	?						SAT-solver based

References

^ C. Baral [2003] Knowledge Representation, Reasoning and Declarative Problem Solving. Cambridge University Press.
^ M. Gelfond [2008] Answer sets. In: Handbook of Knowledge Representation, Elsevier, pages 285-316.
^ Y. Dimopoulos, B. Nebel and J. Köhler [1997] Encoding planning problems in non-monotonic logic programs. In: Proceedings of ECP-97, Springer Verlag, pages 273-285.
^ V.S.Subrahmanian and C. Zaniolo [1995] Relating stable models and AI planning domains. In: Proceedings of ICLP-95, pages 233-247.
^ T. Soininen and I. Niemelä [1998] Formalizing configuration knowledge using rules with choices. Technical Report TKO-B142, Laboratory of Information Processing Science, Helsinki University of Technology.
^ V. Marek and M. Truszczyński [1999] Stable models and an alternative logic programming paradigm. In: The Logic Programming Paradigm: a 25-Year Perspective, Springer Verlag, pages 169-181.
^ I. Niemelä [1999] Logic programs with stable model semantics as a constraint programming paradigm. Annals of Mathematics and Artificial Intelligence, Vol. 25, pages 241-273.
^ Tom Crick (2009) "Superoptimisation: Provably Optimal Code Generation using Answer Set Programming", PhD thesis, Univ Bath.
^ Rogelio Davila, "AnsProlog, an overview"
^ I. Niemelä, P. Simons and T. Soinenen [1999] Stable model semantics of weight constraint rules. In: Proceedings of LPNMR-99, pages 317-331.
^ P. Ferraris and V. Lifschitz [2005] Weight constraints as nested expressions. Theory and Practice of Logic Programming, Vol. 5, pages 45-74.
^ ^a ^b "DLV System company page". DLVSYSTEM s.r.l.. http://www.dlvsystem.com. Retrieved 16 November 2011.